|
Behavioral categories
The behavioral category of a primitive sort specifies the operational behavior of its forms and is assigned in a categorization of the sort's characteristic individual.
Specifically, the behavioral category prescribes the behaviors of forms under common arithmetic operations, their canonical form, and when a form is part of another form:
- Each category specifies the behavior of forms under the operations of sum (combining two forms), difference (subtracting one form from another), and product (intersecting two forms).
- Each category specifies when a form is maximal, that is, has the canonical form. Forms are automatically reduced to their maximal form.
- Finally, each category specifies when a form is part of another form (and when an individual is part of another individual).
Generally, a part-of relationship for each behavioral category forms the basis for the specification of the operational behavior and the maximality of forms,
e.g, the product of two forms is part of both forms, each operand form is part of the sum of these forms, and a form is maximal if no two individuals can be found to be part of a new individual.
However, there is a special category that deviates from this rule and allows the behavior to specified differently.
Behavioral categories are assigned to primitive sorts as part of their characteristic individual.
Composite sorts (either attribute or disjunctive) receive their behavior from their component sorts depending on their compositional relationship:
- The behavior of an attribute sort is, in first instance, the behavior of the base sort.
When individuals combine under any of the arithmetic operations, their attribute forms are combined under the same arithmetic operation.
- The behavior of a disjunctive sort is the behavior of the respective component sorts, for each of the metaform's forms.
When two metaforms combine under any of the arithmetic operations, the respective component forms combine under the same arithmetic operation.
The following examples of behavioral categories are available in the Python sortal library.
- A discrete form is a form with a discrete operational behavioral, corresponding to a mathematical set:
an individual is part of another individual, only if these are identical; a form is part of another form, if every individual of the first form is also an individual of the second form.
The operations of sum, difference and product on forms correspond to set union, difference and intersection, respectively:
under the operation of sum, forms are merged and duplicate individuals are removed; under the operation of product, only identical individuals contribute to the result.
A discrete form is maximal if no two individuals are identical.
In other words, if x and y denote two forms of a sort with discrete behavior, and X and Y denote the respective sets of individuals, then (x : X specifies X as a representation of x)
| x : X ∧ y : Y ⇒ | x ≤ y ⇔ X ⊆ Y |
| x + y : X ∪ Y |
| x − y : X ⁄ Y |
| x · y : X ∩ Y |
In the case of an attribute sort, an individual is part of another individual, only if these are identical and the former's attribute form is part of the latter's attribute form;
a form is part of another form, if every individual of the first form is 'part of' an individual of the second form.
Under the operation of sum, identical individuals have their attribute forms combined under the (corresponding) operation of sum.
Under the operation of product, only identical individuals contribute to the result; their attribute forms combine under the (corresponding) operation of product. The resulting attribute form may be empty.
A discrete form is maximal if no two individuals are identical.
- An interval form is a form with an one-dimensional embedding operational behavior:
an interval is part of another interval if it is embedded in the other interval; a form is part of another form if every interval in the first form is embedded in an interval in the second form.
Under the operation of sum, forms are merged and adjacent (on the same carrier) or overlapping intervals are combined into a single interval;
under the operation of product, the result is composed of the common parts of overlapping intervals.
An interval form is maximal if no two intervals are adjacent (on the same carrier) or overlap.
Let B[x] denote the set of boundary elements of a form x of intervals and, given two interval forms x and y of the same sort,
let Ix denote the set of boundary elements of x that lie within y, Ox the set of boundary elements of x that lie outside of y,
M the set of boundary elements of both x and y where the respective intervals lie on the same side of the boundary element,
and N the set of boundary elements of both x and y where the respective intervals lie on opposite sides of the boundary element; then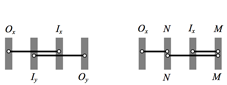
| x : B[x] ∧ y : B[y] ⇒ | x ≤ y ⇔ Ix = ∅ ∧ Oy = ∅ ∧ N = ∅ |
| x + y : B[x + y] = Ox ∪ Oy ∪ M |
| x − y : B[x − y] = Ox ∪ Iy ∪ N |
| x · y : B[x · y] = Ix ∪ Iy ∪ M |
In the case of an attribute sort, an interval is part of another interval if it is embedded in the other interval and the former's attribute form is part of the latter's attribute form.
Under the operation of sum, overlapping intervals are split at the mutual boundary points and identical parts are combined into one, with the attribute forms combined under the (corresponding) operation of sum.
Adjacent intervals (on the same carrier) that have identical attribute forms are also combined.
Under the operation of product, the result is composed of the common parts of overlapping intervals, with the attribute forms combined under the (corresponding) operation of product. The resulting attribute form may be empty.
An interval form is maximal if no two intervals overlap and if adjacent intervals (on the same carrier) have non-identical attribute forms.
- A cyclical form is a form with a one-dimensional cyclical embedding operational behavior. This behavior is quasi-identical to the one-dimensional embedding operational behavior for interval forms as described above, except that for an interval form, all intervals can be ordered based on the starting point of the interval in order to simplify the process of identifying adjacent and overlapping intervals. In the case of the cyclical embedding operational behavior, such ordering must necessarily take into account that the first and last intervals may also be adjacent or overlap.
- An areal form is a form with a two-or-higher-dimensional embedding operational behavior. An areal form behaves similar to an interval form: an areal is part of another areal if it is embedded in the other areal.
Under the operation of sum, forms are merged and areals that overlap or share boundary (on the same carrier) are combined into a single areal. An areal form is maximal if no two areals overlap or share boundary (on the same carrier).
Let B[x] denote the form of boundary segments of a form x of areals (e.g., if x is a form of plane segments, B[x] will be a form of line segments) and,
given two areal forms x and y of the same sort, let Ix denote the form of boundary segments of x that lie within y,
Ox denote the form of boundary segments of x that lie outside of y, M the form of boundary segments of both x and y where the respective areals lie on the same side of the boundary segment,
and N the form of boundary segments of both x and y where the respective areals lie on opposite sides of the boundary segment; then
| x : B[x] ∧ y : B[y] ⇒ | x ≤ y ⇔ Ix = 0 ∧ Oy = 0 ∧ N = 0 |
| x + y : B[x + y] = Ox + Oy + M |
| x − y : B[x − y] = Ox + Iy + N |
| x · y : B[x · y] = Ix + Iy + M |
In the case of an attribute sort, an areal is part of another areal if it is embedded in the other areal and the former's attribute form is part of the latter's attribute form.
Under the operation of sum, overlapping areals are split at their mutual boundaries and identical parts are combined into one, with the attribute forms combined under the (corresponding) operation of sum.
Areals that share boundary (on the same carrier) and have identical attribute forms are also combined. An areal form is maximal if no two areals overlap and if areals that share boundary (on the same carrier) have non-identical attribute forms.
- An ordinal form is a form with an ordinal operational behavior: an individual is part of another individual, only if its ordinal value is smaller than or equal to the latter's ordinal value.
Since, for any two ordinal values, one is always less than or equal to the other, an ordinal form is maximal if it contains only a single individual.
Thus, a form is part of another form, if the former's individual is 'part of' the latter's individual.
Under the operations of sum and product, the resulting form's individual has as ordinal value the largest and, respectively, smallest of both ordinal values.
| x : {m} ∧ y : {n} ⇒ | x ≤ y ⇔ m ≤ n |
| x + y : {max(m, n)} |
| x − y : {} if m ≤ n, else {m} |
| x · y : {min(m, n)} |
In the case of an attribute sort, an individual is part of another individual, if its ordinal value is smaller than or equal to the latter's ordinal value and its attribute form is part of the latter's attribute forms.
Under the operations of sum and product, the resulting form's individual has as ordinal value the largest and, respectively, smallest of both ordinal values, while its attribute form is the result of the respective operation on both attribute forms.
- A special form is a form with a special, ordinal-like behavior. A special behavior must not necessarily be derived from a part-of relationship, though it still specifies when a form is part of another form.
Specifically, considering the sum of two forms, it is not guaranteed that each operand form is part of the resulting form.
A special behavior only applies if two individuals always combine into a single individual, that is, every special form contains at most one individual.
For example, a special behavior applies to colors under the assumption that an entity can only have one color assigned.
However, colors may not necessary adhere to an ordinal behavior which specifies the sum of two color values to be equal to the maximum of both color values.
The specifics of a special behavior is dependent on the characteristic individual it applies to.
Examples
The examples below illustrate the behavior of discrete forms, interval forms, and interval forms where the individuals have attribute forms with discrete behavior.
These examples are expressed in SDL (Sortal Description Language); the symbol '*' denotes the operation of product.
Each highlighted part (with grey background) shows the result of the assignment statement immediately above.
Note that the assignment of data from the sort segments_by_type to the sort typed_segments involves an automatic conversion through the reversal of the object-attribute relationship. More on conversion
sort types : [Label];
sort segments : [LineSegment];
sort segments_by_type : types ^ segments;
sort typed_segments : segments ^ types;
form $types = types: {"wall", "door", "window"};
form $types += types: $types;
{ "door",
"wall",
"window" };
form $types -= types: $types;
{ };
form $wall_segments = segments:
{ <(10,10,0), (50,10,0)>, <(50,10,0), (50,40,0)>,
<(50,40,0), (10,40,0)>, <(10,40,0), (10,10,0)> };
form $window_segments = segments:
{ <(25,40,0), (40,40,0)>, <(50,20,0), (50,30,0)> };
form $segments = segments: $wall_segments + $window_segments;
{ <10(1,1,0), 10(1,4,0)>,
<10(5,1,0), 10(5,4,0)>,
<10(1,1,0), 10(5,1,0)>,
<10(1,4,0), 10(5,4,0)> };
form $segments = segments: $wall_segments - $window_segments;
{ <10(1,1,0), 10(1,4,0)>,
<10(5,1,0), 10(5,2,0)>,
<10(5,3,0), 10(5,4,0)>,
<10(1,1,0), 10(5,1,0)>,
<10(1,4,0), 5(5,8,0)>,
<40(1,1,0), 10(5,4,0)> };
ind $wall = segments_by_type: "wall" $wall_segments;
ind $window = segments_by_type: "window" $window_segments;
form $segments = typed_segments: $wall + $window;
{ <10(1,1,0), 10(1,4,0)>
{ "wall" },
<10(5,1,0), 10(5,2,0)>
{ "wall" },
<10(5,2,0), 10(5,3,0)>
{ "wall",
"window" },
<10(5,3,0), 10(5,4,0)>
{ "wall" },
<10(1,1,0), 10(5,1,0)>
{ "wall" },
<10(1,4,0), 5(5,8,0)>
{ "wall" },
<5(5,8,0), 40(1,1,0)>
{ "wall",
"window" },
<40(1,1,0), 10(5,4,0)>
{ "wall" } };
form $segments = typed_segments: $wall * $window;
{ <10(5,2,0), 10(5,3,0)>,
<5(5,8,0), 40(1,1,0)> };
|
|
|
