|
Terminology
Sortal structures are representational structures based on sorts, a concept for representational flexibility.
Sorts provide a semi-constructive algebraic formalism for design representations (sortal structures)
that enables these to be compared with respect to scope and coverage and that presents a uniform approach to dealing with and manipulating data constructs (sortal descriptions).
Sortal structures, also denoted as sorts, are formal compositions of other, primitive, sortal structures.
While the terms sortal structures and sorts may be used interchangeably, sortal structures emphasize the formal compositional character, while sorts identify the sets of entities, called individuals, represented.
- Sortal structures are class structures, specifying either a single data type or a composition of other class structures.
For instance, data types such as points, labels, and lines all define sorts.
- Sortal structures can also be considered as hierarchical structures of properties, where each property specifies a data type (a primitive sort).
Properties can be collected (a disjunctive sort) and a collection of one or more properties can be assigned as an attribute to another property (an attribute sort).
We distinguish four types of sorts: primitive sorts, attribute sorts, disjunctive sorts and compound sorts.
- A primitive sort specifies a single data type. An individual of a primitive sort has a data value of the specified type.
- An attribute sort is a subordinate, semi-conjunctive composition of a primitive sort (its base) with any other sort (its weight) under the object-attribute relationship.
An individual of an attribute sort is an individual of the base sort (the associate individual) that is assigned a form (a collection of zero, one or more individuals) of the weight sort as an attribute (the attribute form).
If the attribute form is empty, it may be omitted and the individual is treated as an individual of the base sort only, rather than of the attribute sort.
- A disjunctive sort is a co-ordinate, disjunctive composition of any number of sorts under an operation of sum. A form of a disjunctive sort is a composition of forms from the respective component sorts, and is called a metaform.
The representation of each component sort in the composition of forms is optional.
- A compound sort is similar to a disjunctive sort in that it also specifies a disjunctive composition of any number of sorts, however, under an operation of direct product. A form of a compound sort is a composition of (meta)forms from the respective component sorts, and is also considered a metaform.
The representation of each component sort in the composition of forms is optional.
The difference between a disjunctive and a compound sort is mainly conceptual in nature, in that the spatial sorts that form part of a disjunctive sort are considered to occupy the same visual space (or drawing), while the (disjunctive) sorts that form part of a compound sort are considered to specify different visual spaces (or drawings). The difference between disjunctive and compound sorts exceeds the conceptual when we consider the co-habitation of different matching mechanism within a composite sort. Since the geometric components of a disjunctive sort are deemed to occupy the same space, they must adopt the same matching mechanism. On the other hand, the components of a compound sort may each adopt a different matching mechanism.
Each sort may be specified a name, for the purpose of semantic disambiguation. This is a requirement for every primitive sort (or aspect).
Each primitive sort is defined by its characteristic individual, its behavioral category and its matching mechanism.
In addition, the definition of a primitive sort may include one or more arguments, constraining the possible data entities this sort may represent.
For example, the definition of a sort of weights may include the specification of an upper bound for the numeric weight values as argument.
- The characteristic individual defines the representational aspect of a primitive sort, specifically, the representation of its individuals' data values and behavioral methods.
It is specified in its class implementation. Examples of characteristic individuals are points, line segments and labels. More examples
- The behavioral category of a primitive sort specifies the operational behavior of its forms and is assigned in a categorization of the characteristic individuals.
Specifically, the behavioral category prescribes the behavior of forms under common arithmetic operations, their canonical form, and when a form is part of another form.
- The matching mechanism of a primitive sort governs how one of its forms can be found to match another of its forms even if the former is not a part of the latter, in support of emergence and sortal grammars
The behavior (of forms) of a composite sort (whether an attribute or a disjunctive sort) derives from the behavior of its component sorts depending on the compositional relationship.
More on behaviors
Finally, a sortal description is a description of a data construct, expressed as an individual or form (or metaform) of a sort.
- Individuals are the basic elements of a sort, that is, these are the instances of the class structure. For example, a point is an individual of the sort of points.
- A form is a collection of individuals of the same sort, e.g., a set of points.
- A metaform is a collection of forms corresponding the different component sorts of a disjunctive (or compound) sort, e.g., a set of points and line segments.
Example
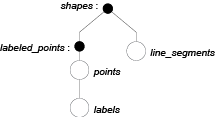
A sort of shapes may be defined as a disjunctive composition of sorts of labeled points and line segments.
A sort of labeled points may be defined as an attribute composition of sorts of points and labels.
The sorts of line segments, points and labels may all be defined as primitive sorts with respective characteristic individuals LineSegment, Point and Label.
An individual line segment is specified by two points (position vectors), indicating the start and end point.
A form of labeled points is specified as a collection of points (each specified by a position vector), each with an attribute form of zero, one or more labels (each specified as a string).
If the attribute form is empty, then it may be omitted.
Points and labels adhere to a discrete (or set) behavior. Combining two forms of labels results in a form of all unique labels.
Combining two forms of labeled points results in a form of all unique points, with for each an attribute form equal to the sum of the respective attribute forms for either original point, if any.
Line segments adhere to an interval behavior; two line segments combine into a single line segment if they share the same co-descriptor (carrier) and are not disjoint.
The co-descriptor of a line segment is the infinite line carrying this line segment.
 In SDL (Sortal Description Language) this example may be described as follows: In SDL (Sortal Description Language) this example may be described as follows:
sort points : [Point];
sort labels : [Label];
sort labeled_points : points ^ labels;
sort line_segments : [LineSegment];
sort shapes : labeled_points + line_segments;
individual $segment = line_segments: <(0,0,0), (100,0,0)>;
form $labelpoints = labeled_points:
{ (0,0,0) {"origin", "start point"}, (100,0,0) {"end point"}, (0,100,0) };
form $shape = shapes: {
line_segments: {<(0,0,0), (100,0,0)>},
labeled_points:
{ (0,0,0) {"origin", "start point"}, (100,0,0) {"end point"}, (0,100,0) }
};
|
|
|
 In SDL (
In SDL (